
Beim Erstellen einer wissenschaftlichen Arbeit ist die Auswertung von Statistiken sehr wichtig. Deshalb erklären wir dir auf unserer Webseite die häufigsten Begriffe, die dir beim Schreiben deiner Bachelorarbeit oder Masterarbeit begegnen können. Der Median ist einer dieser Begriffe – und sobald du ihn kennst, wirst du ihn nicht mehr vergessen, denn eigentlich ist er ganz einfach zu berechnen.
Definition: Median
Das Wort Median stammt aus der englischen Sprache (engl. median) bedeutet auf Deutsch „die Mitte“. Im Zusammenhang mit der Statistik beschreibt der Median den Mittelwert oder mittleren Wert einer Ergebnisreihe.1 2 Er wird deshalb unter anderem auch „Zentralwert“ genannt.
In der Statistik gehört der Median zu den sogenannten statistischen Lagemaßen – zu denen auch das arithmetische Mittel und der Modus gehören. Die Lagemaße geben an, an welcher Stelle (Lage) sich die meisten Daten einer Statistik befinden. So lässt sich mit dem Lagemaß ein ganzer Datensatz anhand einer Zahl (mit einem Wert) zusammenfassen.3 4
Es wird bei der Berechnung des Zentralwertes allerdings unterschieden, ob deine Datenreihe aus einer ungeraden Anzahl von Daten oder einer geraden Anzahl von Daten besteht.
Median: Verwendung
Benötigt wird der Median beispielsweise, um:
- Nach einer Befragung oder Testreihe schnell das Durchschnittsalter zu ermitteln – ohne erst alle Altersangaben addieren und durch die Zahl der Teilnehmer dividieren zu müssen.
- Den Abiturdurchschnitt eines Jahrgangs zu berechnen.
Durch die Anwendung der jeweiligen Formel kommst du schneller zum gewünschten Ergebnis, dem Mittelwert deiner Testreihe.
Median: Formeln
In der folgenden Tabelle werden die zwei Formeln zur Berechnung des Medians wiedergegeben und die benötigten Variablen erklärt.
| Formeln des Medians | |
| Gerade Anzahl an Beobachtungen | |
| Ungerade Anzahl an Beobachtungen | |
| Variablen erklärt | |
| Anzahl an Beobachtungen | |
| Median | |
| Wert aus Datenreihe |
Median: Berechnung
Um den Zentralwert bestimmen zu können, muss deine Zahlenreihe zunächst exakt von der kleinsten bis zur größten Zahl geordnet werden. Mit dem Zentralwert wird der mittlere Wert bestimmt.
In einer Zahlenreihe mit einer ungeraden Anzahl von Werten ergibt sich nach der Sortierung der Werte automatisch eine Zahl in der Mitte der Zahlenreihe. Diese ist dann dein Mittel- oder Zentralwert, den du bei längeren Zahlenreihen aber besser über eine Formelrechnung bestimmen kannst.
Diese Formeln für eine gerade sowie für eine ungerade Anzahl von Daten erklären wir dir hier:
Ungerade Datenanzahl
Anhand der folgenden Beispiele wird deutlich, warum diese Vorgehensweise bei Datensätzen mit Ausreißern bevorzugt wird, denn die Ausreißer fallen dabei nicht ins Gewicht.
Da die Datenreihen kurz sind, ist schnell klar:
- Die jeweils vierte Zahl ist bei diesen Beispielen die mittlere Zahl und bildet den Zentral- oder Mittelwert.
Du musst bei dieser Möglichkeit also theoretisch nicht erst rechnen, um den Median zu erhalten.
Dennoch gibt es selbstverständlich auch dafür eine Berechnungsformel. Diese kannst du oben der Tabelle entnehmen.
Die Anzahl der Daten ist gerade
Bei einer Reihe von 8 Zahlen liegt die Mitte genau zwischen dem vierten und dem fünften Wert deiner Zahlenreihe.
Mathematisch ausgedrückt liegt der Zentralwert hier:
- Zwischen
(hier
) und
- Also:
Um den „Md“ zu errechnen, nimmst du den Wert, der an vierter Stelle steht, und addierst ihn zu dem Wert, der an fünfter Stelle steht. Die Summe teilst du durch die Zahl „2“ und erhältst damit den Median.
Median mithilfe von Excel ausrechnen lassen
Selbstverständlich lässt sich der Median bei größeren Datenmengen auch mithilfe einer Excel-Tabelle ausrechnen. Dafür musst du nur eine neue Tabelle öffnen und deine erhobenen Daten eintragen.
Idealerweise erfolgt die Nummerierung in den Zeilen der ersten Spalte längs am linken Bildrand und die Bezeichnung der jeweiligen Erhebung schreibst du waagerecht als Titel für jede Spalte. Nun trägst du für jede Erhebung die einzelnen Werte sortiert in jedes Feld der Spalte ein.
So hast du beispielsweise in Spalte A und Spalte B jetzt je eine Zahlenreihe stehen.
Median: Schritt-für-Schritt-Anleitung
Im Folgenden erfährst du, wie du den Median mithilfe von Excel berechnest und auswertest.
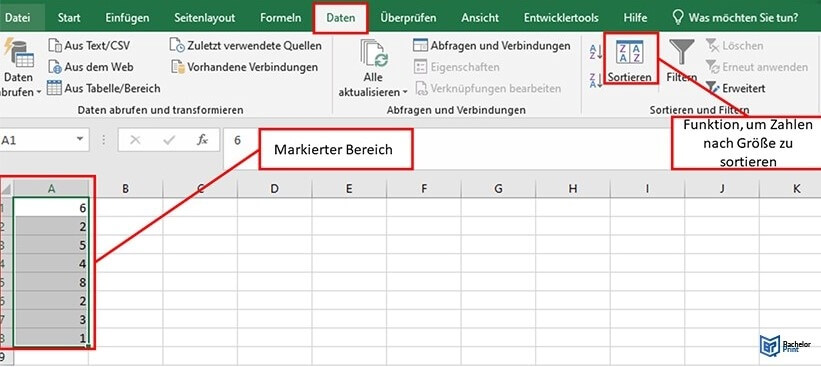
Schritt 1: Daten nach Größe sortieren
Klicke mit der Maus in das erste Feld von Spalte A. Es erhält einen farbigen Rahmen, der anzeigt, dass dieses Feld angeklickt/aktiv ist. Drücke die linke Shift-Taste und klicke mit der rechten Maustaste auf den nach unten zeigenden Cursor-Pfeil auf der Tastatur wie beim Lesen/Scrollen einer Seite.
Damit markierst du alle Zahlen, die in Spalte A sortiert werden sollen – sie werden farbig markiert, sodass du erkennst, ob alle Zahlen erfasst sind.
Mit der Maus klickst du auf den Menüpunkt „Daten“ und anschließend dort auf „sortieren“. Die Zahlen werden automatisch nach Größe sortiert.
Schritt 2: Anzahl der Daten bestimmen
Ob die Anzahl deiner Daten gerade oder ungerade ist, kannst du links an der Zeilennummerierung ablesen und bei einer ungeraden Anzahl die Mitte schnell ermitteln und den Wert ablesen, sodass hier keine Formel notwendig wäre.
Schritt 3: Median mit Formel für gerade oder ungerade Anzahl berechnen, um die Stelle des Medians zu errechnen
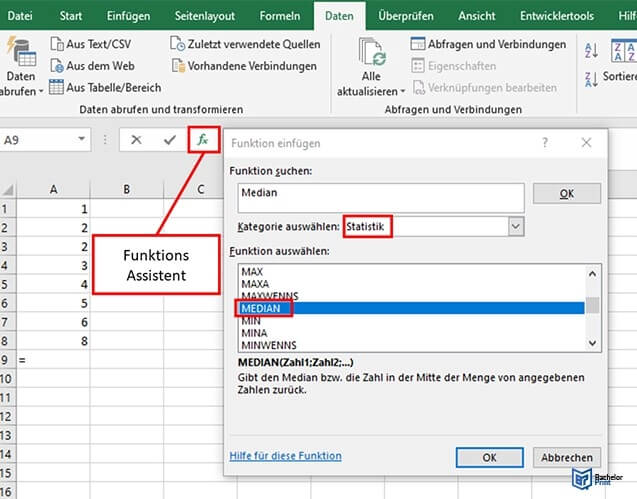
Für eine ungerade Datenzahl klickst du auf das Feld direkt unter deiner Zahlenreihe und in der Menüleiste auf das Zeichen f(x).
Der „Funktions-Assistent“ öffnet sich und du kannst direkt den „Median“ mit einem Doppelklick aus der Liste aller vorgegebenen Funktionen auswählen.
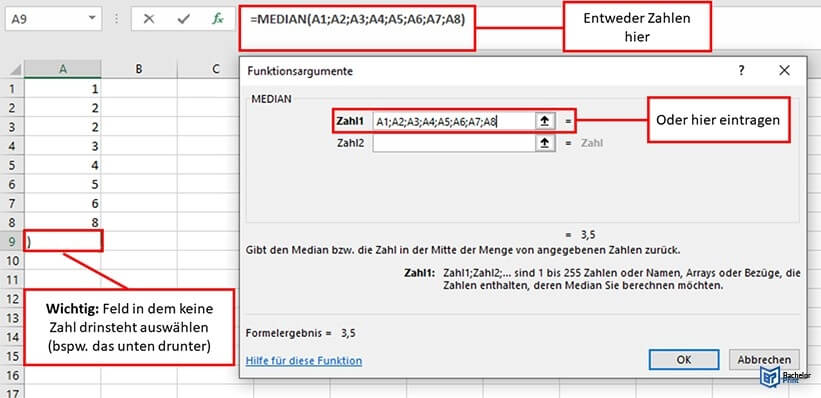
Dabei öffnet sich ein Fenster, in dem „=Median ()“ steht. In die Klammern gibst du nun die zu berücksichtigen Felder ein, indem du sie einzeln der Reihe nach anklickst und mit einem Semikolon trennst. „Enter“ drücken und Excel schreibt dir den Medianwert in das Feld.
Schritt 4: Median an der errechneten Stelle ablesen
Nachdem dir Excel ein Ergebnis abgeliefert hat, solltest du dieses per Hand mit den oben genannten Berechnungsformeln zu überprüfen.
Stimmt es nicht überein, vertraue lieber deiner Berechnung als dem Computer!
Schritt 5: Bedeutung des Ergebnisses interpretieren
Am Ende musst du das Ergebnis interpretieren. Sollte es verschiedenen Auslegungsmöglichkeiten geben, so erwähne diese.
Median, Modus und arithmetisches Mittel
Median, Modus und arithmetisches Mittel gehören zu den Lagemaßen der Statistik.
Median
Der Median ist Mittelwert einer Stichprobenerhebung und vernachlässigt sogenannte „Ausreißer“-Werte der Erhebung mit einer „Ordinalskalierung“.
Modus
Die Werte zur Berechnung des Modus oder Modalwertes wird mithilfe einer „Nominalskalierung“ erhoben.
Der Modus ist der Wert, der in einer Erhebung am häufigsten vorkommt. Er wird oft für sinnvoller erachtet als die Errechnung des Medians oder des Gebrauchs des arithmetischen Mittels.
Arithmetisches Mittel
Die Daten werden mithilfe einer „Intervallskalierung“ erhoben. Das Ergebnis kann ein Wert sein, der nicht in der Wertetabelle vorkommt.
Dadurch, dass hier alle Werte der Erhebung in die Berechnung einfließen, reagiert das Ergebnis des arithmetischen Mittels sensibel auf sogenannte „Ausreißer“-Werte.
Häufig gestellte Fragen
Für den Wert des errechneten Medians.
Beides sind deutsche Wörter für das englische Wort „Median“, das mit dem Wort „die Mitte“ übersetzt wird.
Weil die Mitte zu finden ist.
Diese ist bei einer ungeraden Datenanzahl schnell auszumachen, bei einer geraden Anzahl von Daten liegt der Mittelwert zwischen zwei Datenangaben und muss errechnet werden.
Die Logik erschließt sich aus den beiden mathematischen Formeln, welche sich in der Tabelle unter „Median: Formeln“ finden lässt.
Es steht jeweils für die Gesamtanzahl der vorhandenen Daten. Deshalb ist es wichtig, dass du deine Daten sortierst und eine numerische Reihenfolge festlegst.
Weil das bei langen Zahlenreihen mehr Zeit in Anspruch nimmt als den Median zu errechnen.6
Quellen
1 Duden: Median, in: duden.de, o.D., [online] https://www.duden.de/rechtschreibung/Median (abgerufen am 15.12.2022)
2 Dict.cc: Median, in: dict.cc, o.D., [online] https://www.dict.cc/?s=median (abgerufen am 15.12.2022)
3 Duden Learnattack: Lagemaße, in: learnattack.de, o.D., [online] https://learnattack.de/schuelerlexikon/mathematik/lagemasse (abgerufen am 15.12.2022)
4 Nachhilfe Team: Median berechnen – einfach erklärt (+Übungsaufgaben), in: nachhilfe-team.net, o.D., [online] https://www.nachhilfe-team.net/lernen-leicht-gemacht/median-berechnen/ (abgerufen am 15.12.2022)
5 Microsoft Support: Berechnen des Medians einer Zahlengruppe, in: support.microsoft.com, o.D., [online] https://support.microsoft.com/de-de/office/berechnen-des-medians-einer-zahlengruppe-2e3ec1aa-5046-4b4b-bfc4-4266ecf39bf9 (abgerufen am 15.12.2022)
6 FragMich: Unterschied Median und Durchschnitt, in: Frag doch mich, 02.2022, [online] https://frag-doch-mich.de/online-technik/unterschied-median-durchschnitt/ (abgerufen am 15.12.2022)