Die Spannweite (Range) ist ein Streuungsmaß, welches du im Rahmen der deskriptiven Statistik berechnest. Dir liegt eine Messreihe mit Daten vor, die du auswerten möchtest. Die deskriptive Statistik verschafft dir einen Überblick über die Daten. Anhand der Spannweite erkennst du die Streuung der Daten. Wir zeigen dir, wie du die Spannweite richtig berechnen und in deiner nächsten wissenschaftlichen Arbeit einsetzen kannst.
Spannweite „einfach erklärt“
Die Spannweite ist ein Streuungsmaß und beschreibt die Differenz zwischen dem Maximum und dem Minimum. Um sie zu berechnen, musst du das Minimum vom Maximum deiner Werte abziehen.
Definition: Spannweite
Die Spannweite ist ein aus der Statistik bekanntes Streuungsmaß. Sie ist definiert als die Differenz zwischen dem kleinsten und dem größten Messwert. Der auch als Range bekannte Wert misst die Streuung der mindestens ordinalskalierten Werte.
Wie wird die Spannweite berechnet?
Um die Spannweite zu berechnen, subtrahierst du vom größten Messwert den kleinsten Messwert. Die Einheit des Ergebnisses ist mit der Einheit der Messwerte identisch. Achte darauf, dass alle Messwerte die gleiche Einheit besitzen. Gegebenenfalls ist vor der Subtraktion die Umrechnung erforderlich. Die zugehörige Formel für die Berechnung der Spannweite lautet:
mit R als Range/Spannweite, xmax als dem größten Messwert und xmin als dem kleinsten Messwert.
Berechnungsbeispiel für die Spannweite
Das folgende Beispiel soll die Berechnung der Spannweite veranschaulichen:
Folgende Daten liegen vor:
4m | 5m | 10m | 1m | 7m | 4m | 2m | 5m | 9m |
kleinster Wert: 1m | größter Wert: 10m
Daraus ergibt sich:
10m–1m=9m
⇒ Die Spannweite beträgt 9 Meter
Der Einfluss von Extremwerten
Es besteht keine Robustheit gegenüber Ausreißern, da Extremwerte bei der Berechnung berücksichtigt werden. Ausreißern wird bei der Spannweitenberechnung eine große Bedeutung zuteil. Aussagen über die Verteilung der Messwerte werden dadurch verzerrt.
Aufgrund dieses Umstandes findet die Berechnung der Spannweite vor allem bei kleinerem Stichprobenumfang Verwendung. Je größer der Stichprobenumfang ist, desto geringer ist der Informationsgehalt des Streuungsmaßes.
Beispiel
Folgende Daten liegen vor:
4m | 5m | 10m | 1m | 7m | 4m | 35m | 5m | 9m |
kleinster Wert: 1m | größter Wert: 35m
Daraus ergibt sich:
35m–1m=34m
⇒ Die Spannweite beträgt jetzt 34 Meter, anstelle von den vorherigen 9 Metern. Das zeigt, dass die Spannweite durch einen Ausreißer bereits stark beeinflusst wird.
Die Spannweite mit Excel bestimmen
Excel stellt keine Formel zur Berechnung der Spannweite zur Verfügung. Dennoch ist es möglich, mit Excel die Spannweite zu bestimmen. Dazu verwenden wir wieder die Werte aus unserem Beispiel.
Schritt 1
Trage die Werte in einzelne Zellen ein. Achte darauf, dass jeder Wert in einer einzelnen Zelle steht.
In unserem Fall: Wir tragen die Werte in die Zellen A5 bis I5 ein.
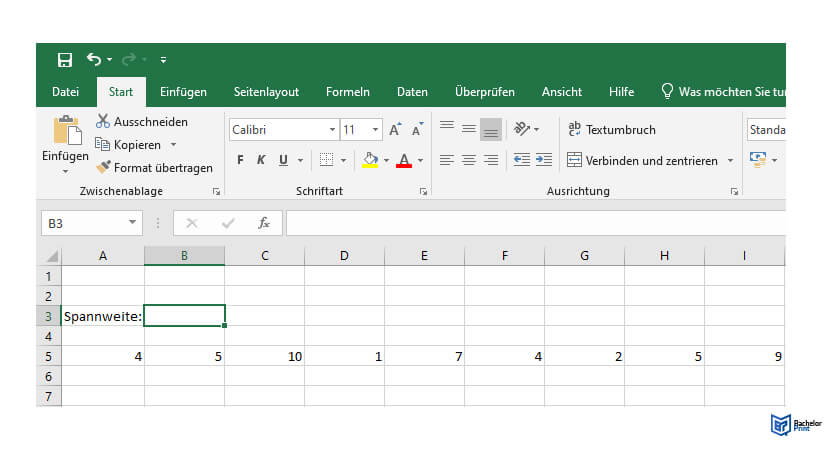
Schritt 2
Wähle eine Zelle aus, in der die Spannweite deiner Werte berechnet und später angezeigt werden soll. Trage in die gewählte Zelle die Formel ein, um die Spannweite berechnen zu lassen.
Formel: MAX(Zelle:Zelle)-MIN(Zelle:Zelle)
Diese Formel besagt, dass das Minimum des Bereichs vom Maximum des Bereichs abgezogen wird.
In unserem Fall: Unsere Werte stehen in den Zellen A5 bis I5. Daher lautet die Formel hierbei: =MAX(A5:I5)–MIN(A5:I5).
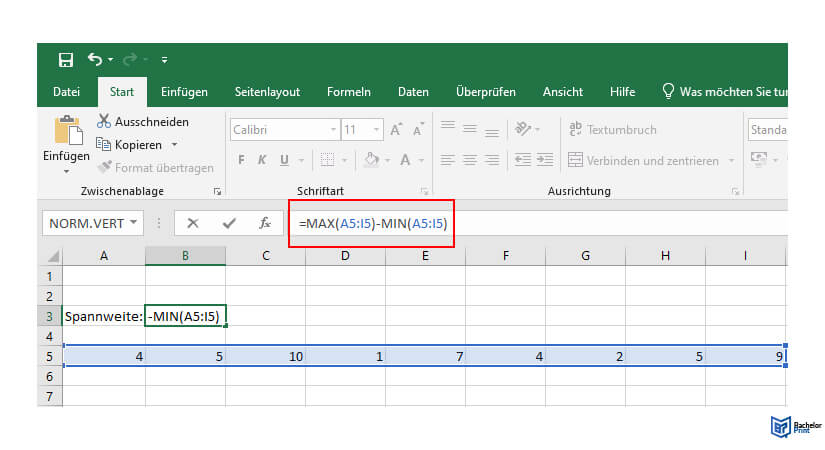
Schritt 3
Bestätige deine Formel mit „Enter“ und die Spannweite deiner Werte wird in der Zelle angezeigt.
In unserem Fall: Es erscheint die Zahl 9. 9 ist somit die Spannweite unseres Beispiels.
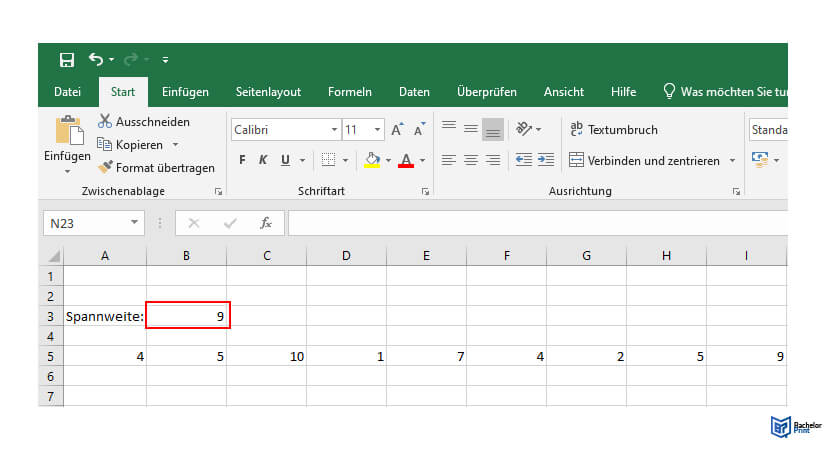
Die Spannweite mit SPSS berechnen
SPSS bietet die Möglichkeit der einfachen Durchführung deskriptiver Berechnungen.
- Unter dem Menüpunkt „Analysieren“ findest du den Unterpunkt „Deskriptive Statistik“.
- Hier wählst du „Häufigkeiten“ aus.
- In der sich öffnenden Box setzt du bei den Kennwerten ein Häkchen, die du wissen möchtest.
- Klicke „Range“ an, dann wird die entsprechende Berechnung durchgeführt.
Häufig gestellte Fragen
Der Range/die Spannweite ist der Abstand zwischen dem kleinsten und dem größten Punkt. Es handelt sich um ein Streuungsmaß.
Die Spannweite ist die Differenz zwischen dem maximalen Wert und dem minimalen Wert. Die Standardabweichung gibt an, um wie viel die Werte im Durchschnitt vom Mittelwert abweichen. Beide Kennzahlen sind Streuungsmaße.1
Nein, die Spannweite ist nicht robust gegen Ausreißer. Extremwerte bestimmen das Ergebnis.
SPSS bietet unter dem Punkt „Analysieren“ die Möglichkeit zur Durchführung von Methoden der deskriptiven Statistik. Wähle den Punkt „Häufigkeiten“ aus, hier findest du den Range.
Du trägst in die Berechnungszeile =MAX(“ „)-MIN(“ „) ein. In die Klammern trägst du die Zellen ein, in denen sich die Messwerte befinden.
Quellen
1 Statista: Definition Standardabweichung, in: de.statista.com, o. D., [online] https://de.statista.com/statistik/lexikon/definition/126/standardabweichung/#:~:text=Die%20Standardabweichung%20ist%20ein%20Ma%C3%9F,Auspr%C3%A4gungen%20eines%20Merkmals%20vom%20Durchschnitt (zuletzt abgerufen am 19.12.2022)
